S03 E04 Détecteurs I et O
Publié le mar. 11 août 2020 dans PQT , modifié le:
Article précédent PQT SO3 E04 Article suivant
Solution de l'exercice précédent
Il s'agissait de calculer les probabilités pour les situations <R❘I> <R❘O> <L❘I> et <L❘O>.
Les calculs vont être un peu plus longs que les précédents, mais pas plus compliqués. Il suffit de ne pas s'embrouiller en prenant le temps de détailler toutes les étapes. Comme promis, ça ne dépassera pas ce qu'on a appris à faire au collège, sauf qu'on y ajoutera les "i" de l'unité imaginaire que nous avons vue dans l'épisode précédent.
Allons-y. Pour le premier, je vais prendre le temps de vraiment détailler toutes les étapes du calcul:
Pour <R❘I> on a l'amplitude de probabilité:
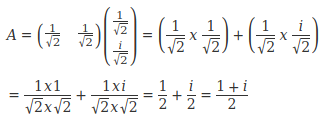
Passons à la probabilité. Souvenons-nous que nous devons multiplier l'amplitude de probabilité par son conjugué:
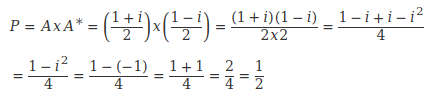
Voilà, comme promis, ce n'était pas tellement plus difficile qu'un calcul de troisième avec des fractions. En revanche, clairement, si nous n'avions pas ajouté aux connaissances de la classe de troisième l'unité imaginaire "i" et la règle des produits hermitiens vues à l'épisode précédent, nous aurions été bien incapables d'aboutir à la bonne probabilité à la fin.
Le monde quantique est comme ça. La nature a décidé qu'on ne pouvait pas l'explorer sans les nombres complexes et les produits hermitiens qui les accompagnent [1].
Solution de l'exercice précédent
Pour <R❘O>, je détaille un peu moins les calculs, mais c'est le même principe:
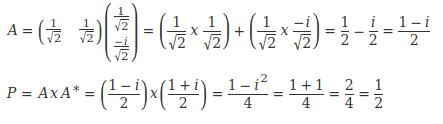
Pour <L❘I>, nous avons:
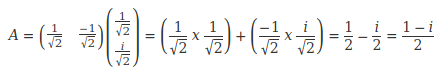
C'est la même amplitude de probabilité que pour <R❘O>, donc aussi la même probabilité.
Et enfin pour pour <L❘O>, nous avons:
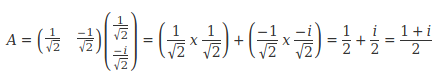
C'est la même amplitude de probabilité que pour <R❘I>, donc aussi la même probabilité.
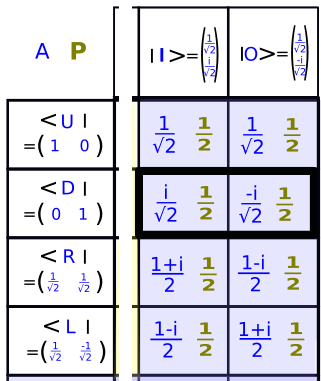
Terminons la grille
Nous pouvons maintenant terminer notre grille. Pour cela, nous devons faire attention à une dernière chose. Comment obtenir le bra, c'est à dire le vecteur ligne, qui correspond à l'état quantique ❘I> ?
Nous devons obtenir une probabilité de 1 pour la situation <I❘I>.
Si nous ne changions rien à nos habitudes, nous aurions:
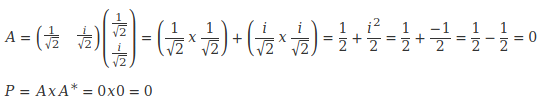
Or ce n'est pas du tout le résultat qu'il nous faut !
Si notre spin est dans l'état ❘I>, nous le détecterons dans l'état ❘I> avec le détecteur <I❘ dans 100% des cas. Donc avec une probabilité de 1 et non pas de 0.
La solution coule de source. De même que nous devons prendre le conjugué quand nous faisons les produits hermitiens, nous devons prendre le conjugué aussi quand nous passons d'un "ket" à un "bra", d'un vecteur colonne à un vecteur ligne.
Autrement dit:
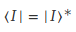
Autrement dit encore, lorsque nous couchons le verteur colonne pour en faire un vecteur ligne, nous devons aussi changer le signe de tous les "i". Dans le cas de notre état quantique ❘I>, ça va donner:
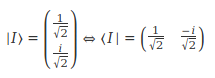
Munis de cette dernière règle, nous pouvons terminer notre grille. Les calculs ne sont pas plus compliqués que les précédents. Je vous propose de terminer vous-même la grille et de vérifier que tout est rentré dans l'ordre. Nous retrouvons toutes les probabilités que nous avions découvertes dans les saisons précédentes.
Nous obtenons:
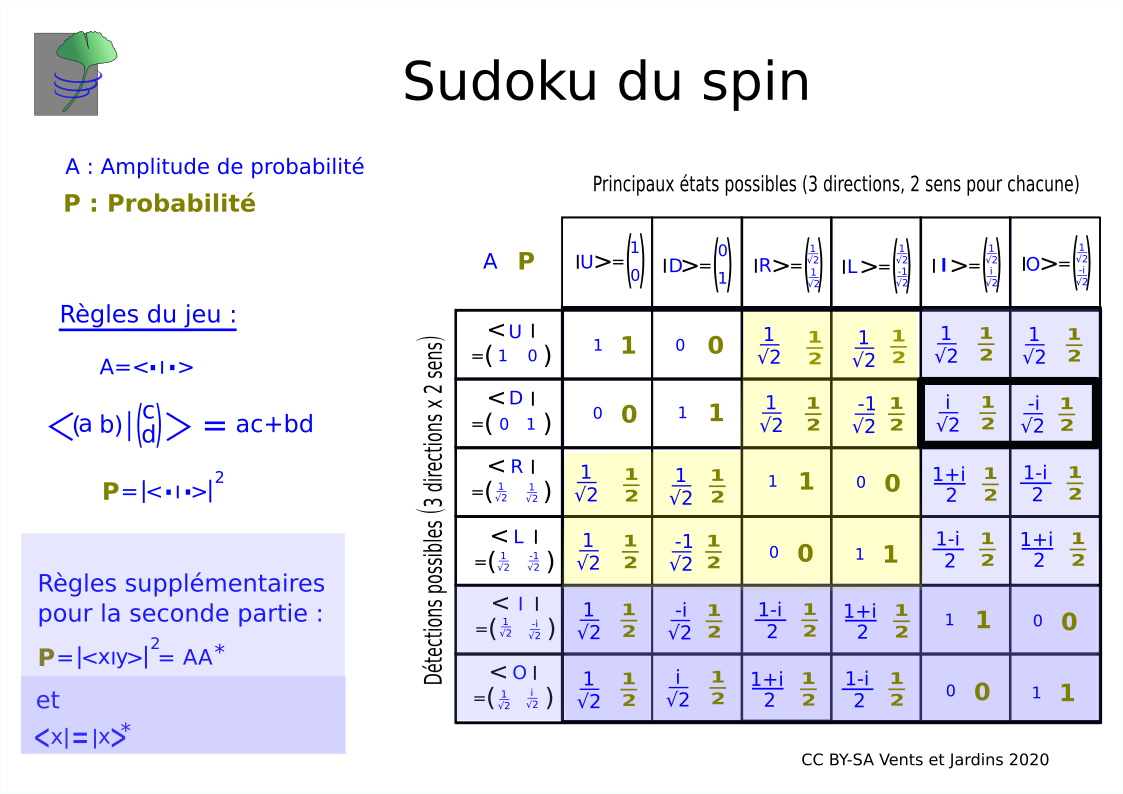
La soution complète du "sudoku"
Un petit point d'étape
Cet exercice nous a permis de réviser un peu les maths du collège et du lycée. Il nous a permis aussi de découvrir le principe étrange des produits hermitiens. Nous commençons à manipuler des amplitudes de probabilités. Bien sûr, si tout ceci ne devait servir qu'à retrouver les résultats que nous connaissons déjà dans l'expérience de Stern et Gerlach, ce serait beaucoup d'efforts pour pas grand chose. Mais il se trouve que la méthode que nous avons développée va nous servir maintenant à pénétrer beaucoup plus loin dans les territoires quantiques.
Et nous voici à présent armés pour jeter un nouveau coup d'œil sur les postulats de la mécanique quantique. C'est ce que nous ferons dans le prochain épisode. Ce nouvel aperçu sera encore largement intuitif, mais il nous permettra de mieux comprendre encore ce que nous étudierons plus en détails dans la saison 04.
Notes et références
| [1] | Ou plus exactement, on pourrait peut-être, mais ça rendrait les calculs beaucoup plus compliqués qu'ils ne le sont déjà. L'utilisation des nombres complexes et des produits hermitiens est naturelle dès lors qu'un phénomène a une nature ondulatoire. Or les phénomènes quantiques ont intrinsèquement ondulatoires, dans le sens où les amplitudes de probabilité "vibrent" et interfèrent entre elles. Nous approfondirons tout ceci dans la saison 04. |
Article précédent PQT SO3 E04 Article suivant