S03 E03 Etats I et O
Publié le mar. 11 août 2020 dans PQT , modifié le:
Article précédent PQT SO3 E03 Article suivant
Solution de l'exercice précédent
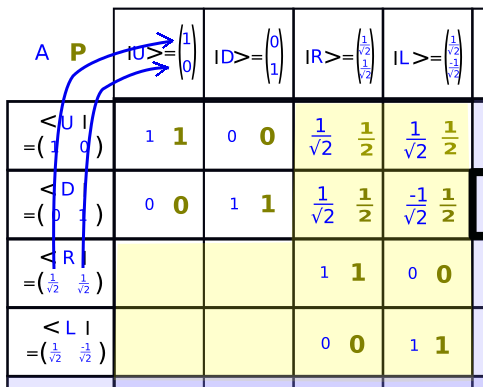
Calcul de <R❘U>
Il s'agissait de remplir les quatre dernières cases jaunes.
On peut assez facilement vérifier que les résultats seront symétriques par rapport à ceux placés en haut et à droite de la figure.
En effet:
Nous avions vu dans l'épisode précédent que pour <U❘R>:
Amplitude de probabilité: A = (1 x 1/√2)+ (0 x 1/√2) = 1/√2
Pour <R❘U> nous aurons de manière symétrique:
A = (1/√2 x 1)+ (1/√2 x 0) = 1/√2
L'amplitude de probabilité de <U❘R> est donc égale à celle de <R❘U>.
Et nous pouvons écrire aussi, avec le même raisonnement:
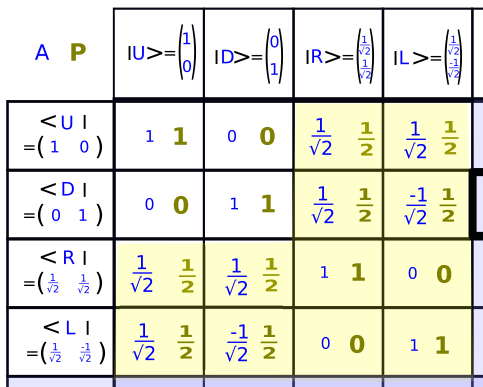
La solution de l'étape 2
- <R❘U> = <U❘R> = 1/√2
- <R❘D> = <D❘R> = 1/√2
- <L❘U> = <U❘L> = 1/√2
- <L❘D> = <D❘L> = -1/√2
Attention à une chose toutefois. Les égalités de ce genre ne fonctionneront pas toujours. Il va nous falloir dans quelques instants leur ajouter une petite subtilité.
Une fois qu'on a les amplitudes de probabilités, il suffit de les élever au carré pour obtenir les probabilités et le résultat suivant:
États ❘I> et ❘O>
Il est temps maintenant de décrire les états ❘I> et ❘O>, qui sont respectivement celui d'un spin qui pointerait directement vers la cible et celui d'un spin qui pointerait directement vers la source.
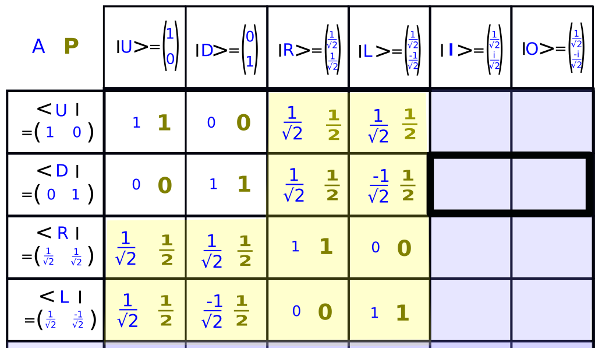
États ❘I> et ❘O>
Nous savons, après nos travaux de la saison 02, quelles probabilités nous devons trouver à la fin. Nous devons notamment trouver:
Pour <U❘I> → 1/2 Pour <D❘I> → 1/2 Pour <U❘O> → 1/2 Pour <D❘O> → 1/2
Et pour cela, nous devons inventer des formules différentes de toutes celles que nous avons déjà utilisées, puisque les états ❘I> et ❘O> sont des états différents de tous les autres.
Attention! Ceci va nous faire rentrer dans le dur du sujet!
En effet, si vous avez fait des essais avec les nombres que nous avons utilisés jusqu'ici, vous vous êtes certainement aperçu qu'il y a toujours un moment où ça cloche. La raison en est simple, c'est tout simplement impossible. Nous pourrions le démontrer, mais nous ne le ferons pas ici [1].
Pour sortir de cette impossibilité, nous allons devoir utiliser des nombres différents de ceux que nous avons appris à l'école: les nombres complexes.
Premier coup d'œil sur les nombres complexes
Nous trouverons des nombres complexes pendant toute la suite de notre voyage. En fait, il n'est tout simplement pas possible de faire de la mécanique quantique sans utiliser des nombres complexes.
À quoi peut-on comparer les nombres complexes? Richard Feynman, dans ses vulgarisations, aimait les présenter comme des "flèches tournantes". C'est ce que nous ferons aussi le moment venu.
Vous vous souvenez peut-être aussi que dans la saison 02 je vous avais dit que d'une certaine manière, les quantités de la physique quantique avaient un angle? Et bien c'est la même idée que celle des "flèches tournantes". Tous ces mystères apparents ne sont en fait que la conséquence de l'utilisation des nombres complexes.
Mais pour commencer, nous allons nous concentrer uniquement sur leur ingrédient fondamental: le nombre imaginaire «i».
Vous savez peut-être que dans l'antiquité, on considérait plus le zéro comme une astuce permettant de marquer une place vide que comme un nombre à part entière? Et bien il en est allé de même au début pour le «nombre i», appelé aussi parfois «l'unité imaginaire» qui est apparu historiquement en Italie au milieu du XVIème siècle. Au début, il n'était considéré que comme une astuce de calcul. Il a fallu plusieurs siècles avant qu'il soit considéré comme un véritable nombre, d'un genre nouveau.
Pour nous et pour le moment nous n'avons besoin que d'une manière de le définir. Nous ne commencerons à explorer les innombrables conséquences de cette révolution conceptuelle, car c'est bien une véritable révolution dans les sciences, que petit à petit.
Pour le moment donc, contentons-nous de décider que:
i² = -1
C'est tout ?
C'est tout! Toute la révolution des nombres complexes découle ensuite logiquement de cette petite décision et c'est tout ce que nous avons besoin de savoir pour le moment.
Arrêtons-nous quand même encore un instant sur cette "petite" décision:
Ce n'est quand même pas rien, ce que nous venons de poser! Parce que vous pouvez essayer de vérifier avec tous les nombres que vous avec appris jusqu'à la fin du collège, aucun d'entre eux n'est capable de réaliser cet exploit. Le nombre un multiplié par lui-même donne un, et le nombre négatif moins un multiplié par lui-même donne aussi un. Nous venons donc d'imaginer un nouveau nombre, doté de cette capacité incroyable: i x i = -1 et nous l'appelons l'unité imaginaire. C'est lui qui va nous permettre de poursuivre la suite de notre voyage en pays quantique. Sans lui ça ne serait pas possible [2].
La solution pour les états ❘I> et ❘O>
Sans l'unité imaginaire "i", il n'y avait pas de solution possible pour la suite de notre sudoku. Munis de l'unité imaginaire "i", il y en a plusieurs [3]. C'est une situation qu'on rencontre souvent en physique: Il y a plusieurs manières mathématiques de décrire une même situation physique et toutes donneront les bons résultats. Dans ce genre de cas, il est tout naturel de prendre celle qui est la plus facile à écrire. Les physiciens appellent ça «choisir un référentiel» et il essayent toujours de choisir le référentiel dans lequel les calculs seront les plus faciles.
Dans notre cas, le voici:
Nous écrirons les états quantiques ❘I> et ❘O> ainsi:
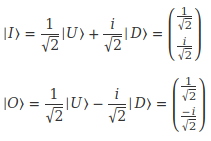
Prenez le temps de les comparer aux formules pour les états ❘R> et ❘L> que nous avons étudiés lors de l'épisode précédent. Notre panoplie d'états quantiques pour cette saison est désormais complète. Observez les similitudes et les différences.
Deux cases de plus
Notre panoplie d'états quantiques est complète, mais il reste encore des cases vides dans notre sudoku et il faut maintenant nous en occuper. Nous procéderons exactement comme dans l'épisode précédent.
Commençons par les cases <U❘I> et <U❘O> :


Jusque là, tout va bien.
Et un gros souci avec la suivante !

??!?!? Ça, c'est la cata !!!
On ne le répétera jamais assez: Ça n'existe pas les probabilités négatives !!!
Il y a quelque chose qui cloche! Et ce quelque chose, c'est que quand on utilise des nombres complexes, on doit modifier certaines des règles que nous avons utilisées jusqu'ici. C'est ce que nous allons voir maintenant. Produit scalaire et produit hermitien
Pour continuer notre progression, nous allons devoir maintenant introduire un peu de vocabulaire nouveau.
Les calculs que nous avons faits jusqu'à présent pour trouver nos amplitudes de probabilités ont un nom savant en mathématiques: On appelle ça des produits scalaires.
Mais à partir du moment où on commence à mettre dans nos équations des nombres complexes, comme on vient de le voir, les produits scalaires ne donnent plus les bons résultats. La raison de tout cela est profonde et on y reviendra de manière plus approfondie dans la saison 04. Pour le moment, nous faisons nos premières gammes, donc nous allons aller directement à la solution.
Quand on utilise des nombres complexes dans nos calculs d'amplitudes de probabilités, nous devons remplacer nos produits scalaires par quelque chose de plus subtil et qui s'appelle un produit hermitien en l'honneur du mathématicien Charles Hermite (1822-1901) qui a découvert tout ça.
Le principe du produit hermitien est simple: Au lieu de multiplier un nombre complexe par un autre, on le multiplie par son conjugué.
Et c'est quoi son conjugué ?
C'est exactement le même nombre, sauf qu'on change le signe de son "i". Et s'il y a plusieurs nombres, comme pour nos états quantiques, on change le signe partout où il y a des "i".
Quelques exemples valent mieux qu'un long discours:
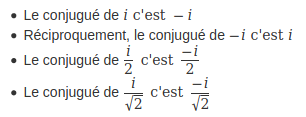
Vous avez compris le principe.
Dernière petite nouveauté à mémoriser dans cet épisode, le conjugué d'un nombre complexe se note en lui mettant une petite étoile, ainsi:
Si notre nombre complexe se note A, sont conjugué se notera A*.
Donc à partir de maintenant, quand nous calculons les probabilités, au lieu de multiplier l'amplitude de probalité par elle-même, nous allons la multiplier par son conjugué.
Autrement dit, là où nous faisions:
P = A² = A x A
Nous devrons dorénavant faire:
P = A x A*
Évidemment, s'il n'y a pas de "i" dans l'amplitude de probabilité, ça ne changera rien, il n'y aura rien à modifier. Tous nos calculs précédents restent donc valides. En revanche chaque fois qu'il y aura un "i" dans l'amplitude de probabilité, il faudra changer son signe dans l'un des deux exemplaires avant de faire la multiplication.
Solution pour les cases <D❘I> et <D❘O>
Reprenons maintenant nos calculs en remplaçant les produits scalaires par des produits hermitiens.

Cette fois-ci, c'est bon! Notre probabilité a retrouvé un signe positif!
Ça a été un peu laborieux, mais vous vous y ferez vite. Derrière tous ces calculs d'apparence compliquée au début, vous découvrirez progressivement une manière de faire très abstraite, très différente de ce qui se passe dans notre quotidien, mais finalement très cohérente et pas si difficile que ça. C'est là que se situe le vrai cœur du "mystère" quantique: Nous devons utiliser des nombres complexes et donc des produits hermitiens, parce que la nature en a décidé ainsi et que le monde quantique fonctionne de cette manière. Au début c'est déstabilisant, mais vous verrez, on s'y fait assez vite.

Travail à la maison
Muni de notre produit hermitien, vous pouvez maintenant calculer tout seul les probabilités pour les situations <R❘I> <R❘O> <L❘I> et <L❘O>. Ce n'est pas très difficile à faire et ça vous fera un excellent entraînement pour la suite. Comme vous le savez, vous devez trouver à chaque fois une probabilité de 1/2.
Toutefois, ce petit «travail à la maison» va vous demander de réviser un peu les maths apprises au collège. Vous allez vous retrouver avec un mélange de nombres habituels et de «i» dans des fractions. Ceci ne doit pas vous effrayer, faites vos calculs comme on vous l'a appris au collège et tout à fait à la fin vous remplacerez les «i²» par des «-1» avant de simplifier.
Et si vous n'y parvenez pas, ça n'est pas très grave. Prenez au moins le temps d'essayer. Nous nous retrouverons dans le prochain épisode pour voir ensemble la solution puis terminer notre grille.
A bientôt !
Notes et références
| [1] | Ceux qui disposent du livre de Leonard Susskind trouveront au chapitre 2 un exercice qui les guidera dans cette démonstration. |
| [2] | Certains puristes diront peut-être qu'on pourrait essayer de s'en passer, mais il faudrait pour ça inventer des méthodes encore plus compliquées et qui reviendraient exactement au même à la fin. Est-ce que ces méthodes compliquées sont la même chose que notre nombre i, exprimé sous une forme plus compliquée, ou est-ce qu'elles sont d'une autre nature? C'est là un débat mathématico-philosophique de très haut niveau dans lequel nous ne nous risquerons pas. |
| [3] | Si vous essayez à la fin, vous les trouverez facilement. |
Article précédent PQT SO3 E03 Article suivant