S03 E05 Second coup d'œil sur les postulats

Principe de superposition

L'état d'un système quantique est défini par un vecteur qui est une combinaison linéaire, avec des coefficients complexes, d'états de base.

Nous avons déjà vu un exemple caractéristique de ceci avec les états |I> et |O>.

L'état "I" de notre spin est défini par le vecteur d'état |I>.

Cet état est une combinaison des deux états de base de notre système. Nous avons choisi d'exprimer tous les états possibles de notre spin en fonction des probabilités qu'il aurait d'être détecté aligné vers le haut (détecteur <U|) ou aligné vers le bas (détecteur <D|).

Nos deux états de base sont donc |U> et |D>.

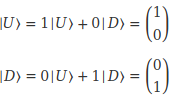
Tous les autres états, comme ici |I> et |O> sont définis en ajoutant une certaine quantité de l'un et une certaine quantité de l'autre. En mathématique, on appelle ce genre de chose une combinaison linéaire. Nous en apprendrons beaucoup plus sur les combinaisons linéaires dans la saison 04, car elles ne font pas partie de programme de mathématiques du collège, mais nous commençons dès à présent à comprendre de quoi il s'agit.

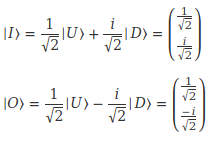
Les coefficients de cette combinaison linéaire de deux états de base, autrement dit la quantité de chacun d'entre eux, sont des nombres complexes. En fait, dans l'exemple ci-contre, on pourrait argumenter en disant que seule la quantité de |D> est définie par un nombre complexe. La quantité de |U> est une quantité ordinaire, définie par le nombre ordinaire 1/√2, qui est un nombres "réel". En fait, l'appellation "nombres complexes" fonctionne comme des poupées russes. Un nombre complexe a deux parties, une partie normale, réelle, plus une certaine quantité de "i", qu'on appelle sa partie complexe. Un nombre "ordinaire" est donc aussi un nombre complexe. Simplement, sa partie imaginaire est à zéro. À l'inverse, un nombre dit "imaginaire pur" est un nombre dont la partie réelle est à zéro. Au total, on considère donc que les nombres ordinaires, "réels", sont un sous-ensemble des nombres complexes.

Une combinaison linéaire comme celle qui définit les états |I> et |O> peut s'écrire sous la forme d'un "vecteur colonne" comme à la droite des équations. C'est quoi un "vecteur" et c'est quoi ces vecteurs qui ont des coefficients complexes? Ça, ça nous emmènerait un peu loin pour le moment, on en reparlera dans la saison 04.

Relisez maintenant le premier postulat de la mécanique quantique, normalement, maintenant, vous devez le comprendre, au moins dans son principe.

Principe de correspondance

Les observables physiques (c'est-à-dire les «choses qu'on mesure») sont représentées par des opérateurs mathématiques.

Une «observable», c'est par exemple la position d'une particule. Ou l'orientation d'un spin. Les observables sont représentées par des opérateurs mathématiques. Les plus simples de ces opérateurs mathématiques, nous les découvrirons dans la prochaine saison, sont de simples tableaux de quatre nombres. Mais bien sûr, il y en a d'autres qui sont beaucoup plus compliqués.

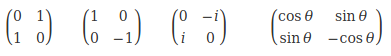
Ces objets mathématiques s'appellent des «opérateurs» car ils fonctionnent comme des machines. Si vous faites rentrer dedans un vecteur, il en ressortira un autre vecteur.

Mais ils ont une autre propriété qui nous sera utile dans la prochaine saison et dont nous allons parler en avant-première dans un instant. Si on les manipule bien, ils vont accoucher de nos vecteurs de base et tous les résultats possibles de n'importe quelle mesure.

Inversement, ces opérateurs ne tombent pas du ciel: Si nous connaissons déjà les états de base et les valeurs possibles pour les mesures, nous pouvons reconstruire l'opérateur qui les synthétise. C'est d'ailleurs ainsi que procède Leonard Susskind dans le chapitre 3 de son cours.

Principe de quantification

Les mesures ne peuvent pas donner d'autres résultats que ceux qui correspondent à des valeurs propres de ces opérateurs mathématiques. Les vecteurs propres qui correspondent à ces valeurs propres forment une base de l'espace des états de ce système.

C'est la suite du postulat précédent. Si je manipule bien l'opérateur qui représente la mesure du spin, je vais obtenir:

1. Ce qu'on appelle ses valeurs propres. Il n'y en a que deux dans le cas du spin: +1 et -1. Vous me direz peut-être que vous avez vu des articles sur le spin disant que les deux valeurs possibles sont +1/2 et -1/2 ? Voire même +ℏ/2 et -ℏ/2 ? En fait ça revient au même, l'important ici c'est que ces deux valeurs sont symétriques et qu'il n'y en a que deux. Si je change d'unité de mesure et que je décide de mesurer les énergies par référence à la coudée égyptienne à la place des mètres, le nombre qui exprime le résultat de ma mesure changera aussi. Exactement comme si d'un seul coup, je décidais d'exprimer la vitesse de ma voiture en miles par heure et plus en kilomètres par heure. Derrière cette différence apparente, la physique, elle, ne change pas. Les deux résultats possibles restent égaux en valeur mais de signe contraire, comme dans notre expérience de Stern et Gerlach. Il n'y en a pas d'autres.
2. Ce qu'on appelle les vecteurs propres de l'opérateur. Ce sont nos vecteurs d'état de base. Ils vont nous permettre de définir tous les autres états du système. Dans le cas du spin, ce sont bien sûr:

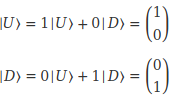
Nous comprenons maintenant le principe de quantification, au moins dans le cas particulier du spin.

Règle de Born

Les calculs mathématiques fournissent la probabilité d'observer tel ou tel résultat de mesure.

La règle de Born, dans le cas du spin, c'est ce que nous n'avons pas cessé de faire avec notre "sudoku du spin".

Résumons-nous:

1. A partir de l'opérateur mathématique du spin (un tableau de 4 expressions mathématiques que nous verrons dans la saison 04), on obtient (par une méthode que nous verrons aussi dans la saison 04) les résultats possibles (+1 et -1) et les vecteurs de base (|U> et |D>).
2. Avec ces vecteurs de base, nous pouvons, par une combinaison linéaire, obtenir tous les autres vecteurs d'état, afin de représenter tous les états possibles de notre spin.
3. Et en faisant les calculs avec des produits hermitiens comme nous l'avons fait dans notre sudoku, nous obtenons les «amplitudes de probabilités» dont le carré donne la probabilité d'obtenir tel ou tel résultat.

Nous comprenons donc désormais la règle de Born.

principe de réduction du paquet d'onde

La mesure modifie l'état du système quantique mesuré de manière à faire disparaître les probabilités qui ne se sont pas réalisées.

Et ça, on l'a déjà vu dès la saison 02. Une fois qu'un état "mélangé" a été détecté dans une position quelconque, il n'est plus dans l'état mélangé. Il a été entièrement "projeté" dans l'état dans lequel il a été détecté. Nous avons vu ça si souvent que je n'y reviens pas ici.

Nous comprenons maintenant le principe de la réduction du paquet d'onde dans le cas particulier du spin, même si nous ne savons pas encore pourquoi ce principe porte un nom aussi bizarre.

Équation de Schrödinger

L'évolution dans le temps du système quantique est fixée par l'équation de Schrödinger.

Bon, là, je vais vous décevoir un peu. Ce dernier postulat, nous n'avons pas encore de quoi le comprendre. En deux mots, il décrit comment nos vecteurs d'état évoluent au cours du temps.

Je vais quand même essayer de vous en donner une idée dès à présent, car elle nous resservira dans l'épisode consacré au fentes de Young. Il se trouve que les amplitudes de probabilités, comme nous l'avons vu dans le sudoku, sont des nombres complexes. Et il se trouve que les nombres complexes peuvent être représentés par des petites flèches. Et enfin, il se trouve que dans le cas de l'expérience des fentes de Young, l'équation de Schrödinger nous dit que ces petites flèches imaginaires avancent en tournant.

On aura l'occasion d'y revenir dès le prochain épisode.

Article précédent   PQT SO3 E05   Article suivant